TASA DE RENDIMIENTO

Esta medida contable representa la razón de las utilidades anuales promedio después de impuestos respecto de la inversión en el proyecto. En el ejemplo anterior sobre, la nueva máquina, las utilidades anuales promedio en libros para el periodo de cinco años son $2 100,y la inversión inicial en el proyecto es de $18 000. Por tanto, tenemos que la
  
Tasa promedio de rendimiento = 2100 /18000 = 11.67 % (6.1)

Si el ingreso fuera variable durante los cinco años, se calcularía un promedio que se utilizaría en el numerador. Una vez que se ha calculado la tasa promedio de rendimiento para una propuesta, se le puede comparar con la tasa de rendimiento requerida para determinar si se debe aceptar o rechazar una propuesta específica.

La principal ventaja de la tasa promedio de rendimiento es su sencillez utiliza la información contable fácilmente accesible. Una vez que se ha calculado la tasa promedia de rendimiento para una propuesta, se puede comparar con una tasa de rendimiento requerida, o de corte, para determinar si se debe aceptar o rechazar una propuesta específica. Las desventajas principales del método son que se basa en el ingreso contable en lugar de los flujos de efectivo, y que no toma en cuenta la periodicidad con que tienen lugar los ingresos y egresos de efectivo. Se pasa por alto el valor del dinero en el tiempo: se valoran los beneficios del último año igual que los beneficios del primer año.

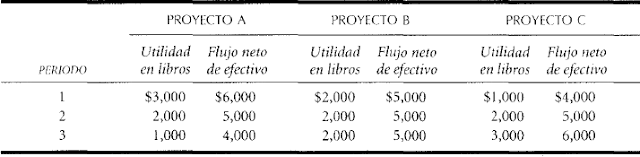
Supongamos que tenemos tres propuestas de inversión, que cuesta $9 000 cada una y tienen una duración económica y depreciable de tres años. Supongamos que esas propuestas esperan proporcionar las siguientes utilidades en libros y flujos de efectivo durante los próximos tres años.

Cada propuesta tendrá la misma tasa promedio de rendimiento: $2000/ $9 000, o 22.22% sin embargo, serían pocas las compañías, en caso de haberlas, que consideraran los tres proyectos como igualmente favorables. Tal vez la mayoría preferiría el proyecto A, que proporciona una mayor parte de sus beneficios totales de efectivo durante el primer año. Por esta razón, la tasa promedio de rendimiento deja mucho que desear como método para la selección de un proyecto.

La ganancia anual que tiene cada inversionista se puede expresar como una tasa de rendimiento o de ganancia anual llamada tasa interna de rendimiento. En la gráfica 3.2 se observa que, dado que la tasa de interés, que en este caso es la TMAR, es fijada por el inversionista, conforme ésta aumenta el VPN se vuelve más pequeño, hasta que en determinado valor se convierte en cero, y es precisamente en ese punto donde se encuentra la TIR.

TIR es la tasa de descuento que hace el VPN = O.

Ecuación 3.3

Al igualar el VPN a cero, la única incógnita que queda es la i. Esta tasa se obtiene por iteración o de manera gráfica. Obsérvese de la gráfica 3.2 quela curva cruza el eje horizontal a un valor aproximado a 21 %. El valor de la TIR para el ejemplo 3.1 es exactamente 20.76006331%.

FUENTE:
http://admonyeconomia.blogspot.mx/2012/11/tasa-de-rendimiento.html
http://www.econlink.com.ar/economia/criterios/tir.shtml

COMENTARIOS: 

La TIR (Tasa Interna de Retorno) es aquella tasa que hace que el valor actual neto sea igual a cero. 

Algebraicamente: 

VAN = 0 = Σi=1...n BNi / (1+TIR)i 

La regla para realizar una inversión o no utilizando la TIR es la siguiente: 

Cuando la TIR es mayor que la tasa de interés, el rendimiento que obtendría el inversionista realizando la inversión es mayor que el que obtendría en la mejor inversión alternativa, por lo tanto, conviene realizar la inversión. 

Si la TIR es menor que la tasa de interés, el proyecto debe rechazarse. 

Cuando la TIR es igual a la tasa de interés, el inversionista es indiferente entre realizar la inversión o no.